Conventional crystals have a repeating unit, the unit cell, which is periodically arranged. Quasicrystals on the other hand are not periodic, but still ordered. The most intuitive example is probably a Penrose tiling in two dimensions. Here instead of one unit, one has two tiles, and a set of construction rules. This allows to fill the entire 2D plane.

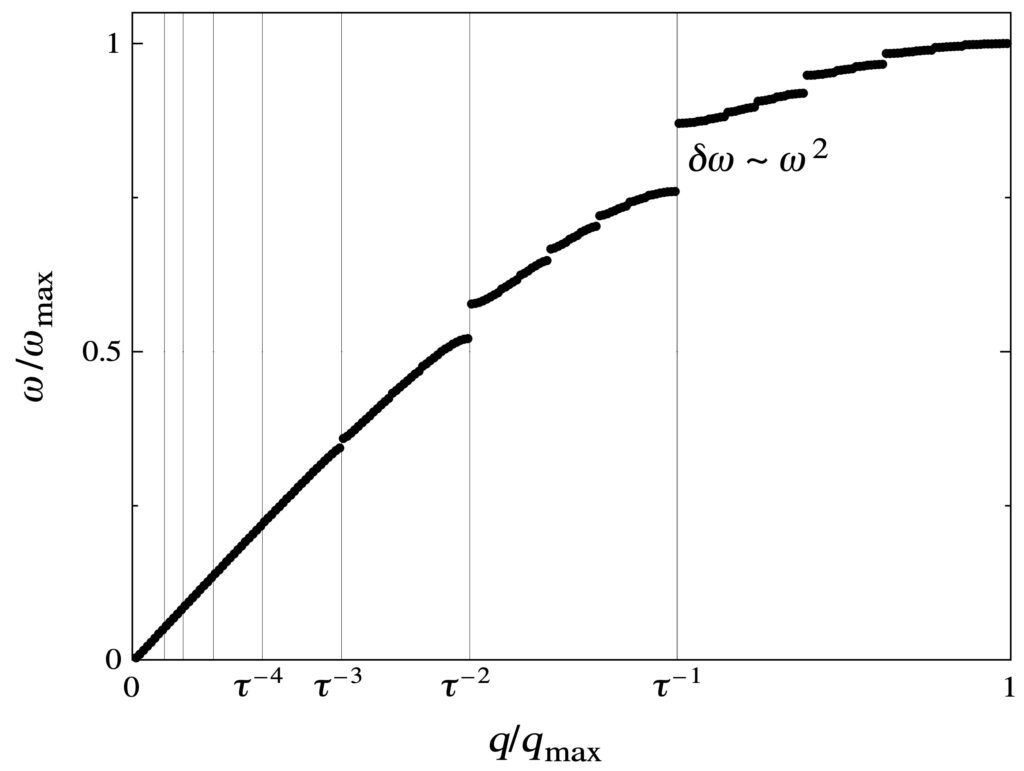
The structure of quasicrystals is self similar in can be scaled by the golden ratio. For the physical properties the consequence is that for the phonon or spectrum of acoustic excitations, instead of having one gap at the boundary of the Brillouin zone, one has a geometric series of gaps.

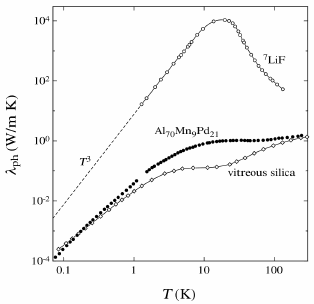
The wave-vector of a phonon in a crystal is only defined modulo the size of the unit cell. This leads to to limiting the thermal transport by a scattering process called Umklapp scattering, which in crystals gives rise to a maximum in the thermal conductivity of the phonons and and exponential decay towards very high temperatures. In quasicrystals on the other hand, there is now a geometric series of sizes, which permit Umklapp scattering, leading to a much shallower maximum and a powerlaw decay of the thermal conductivity towards the highest temperatures. This puts the thermal conductivity of quasicrystals in between that of crystals and amorphous materials.