Apéridicité

Les cristaux conventionnels ont une unité répétitive, la cellule unitaire, qui est disposée périodiquement. Les quasi-cristaux, en revanche, ne sont pas périodiques, mais néanmoins ordonnés. L’exemple le plus intuitif est probablement un pavage de Penrose en deux dimensions. Ici, au lieu d’une unité, on a deux tuiles et un ensemble de règles de construction. Cela permet de remplir tout le plan 2D.
Similarité avec soi
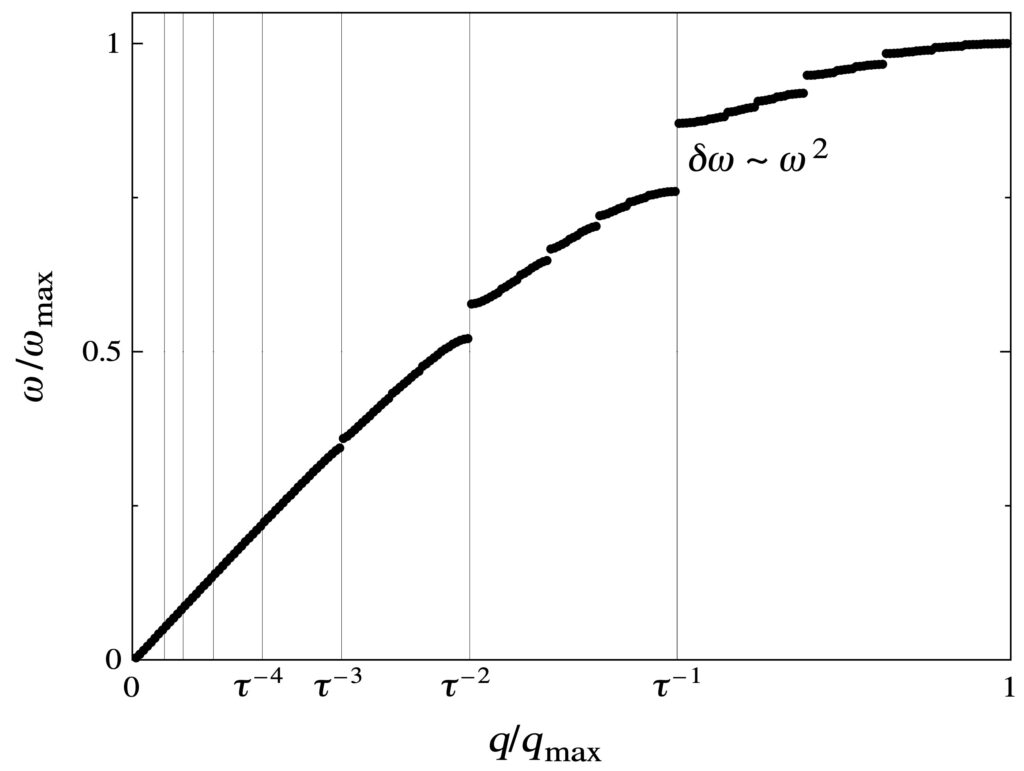
La structure des quasi-cristaux est similaire et peut être mise à l’échelle par le nombre d’or. Pour les propriétés physiques la conséquence est que pour le phonon ou spectre des excitations acoustiques, au lieu d’avoir un gap à la limite de la zone de Brillouin, on a une série géométrique de gaps.
Diffusion Umklapp
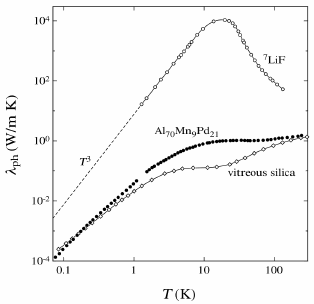
Le vecteur d’onde d’un phonon dans un cristal n’est défini que modulo la taille de la maille unitaire. Cela conduit à limiter le transport thermique par un processus de diffusion appelé diffusion Umklapp, qui dans les cristaux donne lieu à un maximum de conductivité thermique des phonons et à une décroissance exponentielle vers des températures très élevées. En revanche, dans les quasi-cristaux, il existe désormais une série géométrique de tailles qui permettent la diffusion d’Umklapp, conduisant à un maximum beaucoup plus faible et à une décroissance en loi de puissance de la conductivité thermique vers les températures les plus élevées. Cela place la conductivité thermique des quasi-cristaux entre celle des cristaux et des matériaux amorphes.
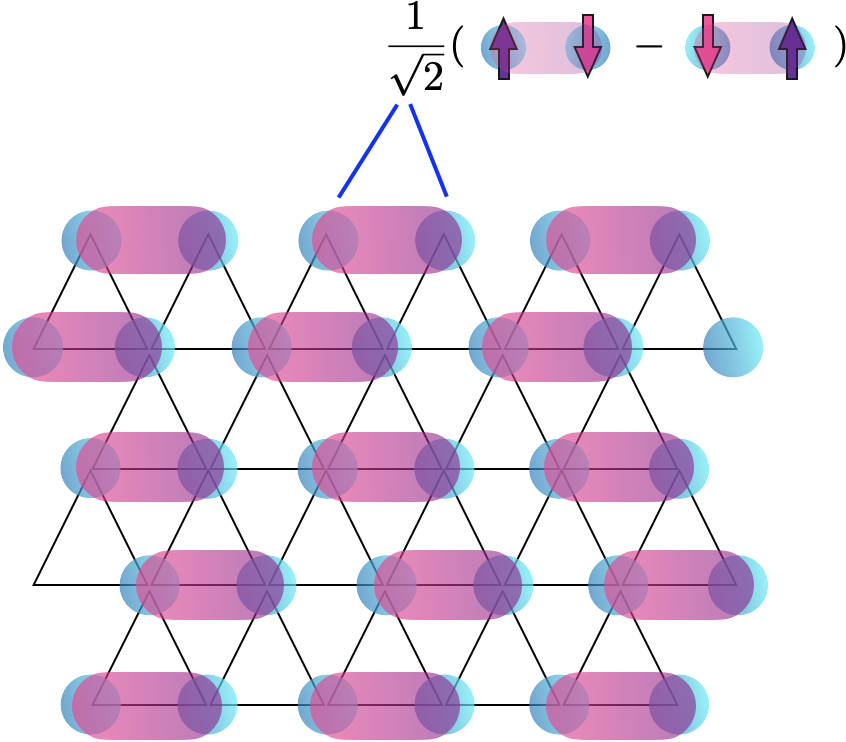
 en_US
en_US