Frustration magnétique

L’étude de la frustration dans les systèmes magnétiques remonte au problème géométrique qui se pose lorsqu’on tente de placer trois spins avec des interactions antiferromagnétiques sur un triangle. L’interaction entre les atomes voisins favorise un alignement antiparallèle entre deux spins voisins, une condition qui est impossible à satisfaire. En conséquence, malgré l’interaction, les spins demeurent dans un état fluctuant jusqu’aux températures les plus basses. L’exemple le plus connu d’un tel système est l’état appelé « glace de spin » pour les atomes magnétiques situés sur les tétraèdres partageant les coins dans la structure de la pyrochlore.
Entropie enorme
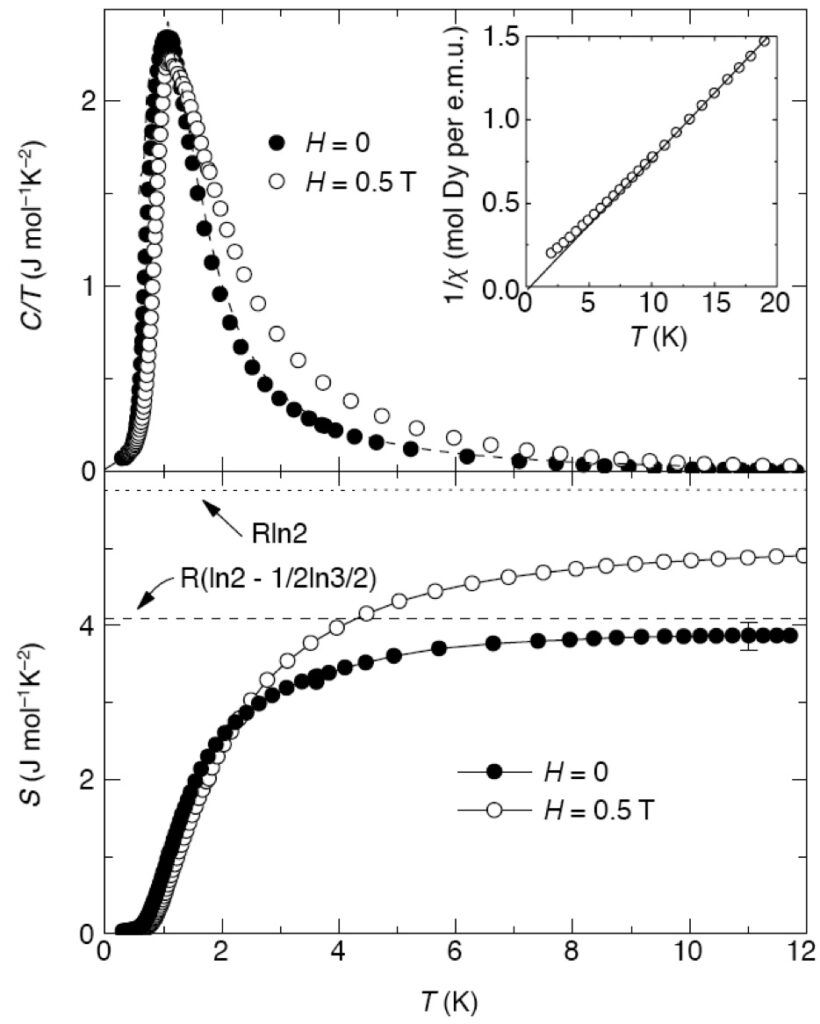
Ces types de systèmes ont attiré beaucoup d’attention lorsqu’on s’est rendu compte qu’ils présentaient une grande entropie résiduelle à des températures nulles. Cette entropie est le résultat des nombreuses orientations de spin possibles autorisées sur un tel réseau : pour réaliser les interactions antiferromagnétiques, deux spins doivent être placés pointant vers le tétraèdre et deux spins pointant vers l’extérieur du tétraèdre. Ce problème correspond au problème de la position des atomes d’hydrogène par rapport à l’oxygène dans la phase cubique de la glace d’eau (H2O), d’où le nom de glace de spin.
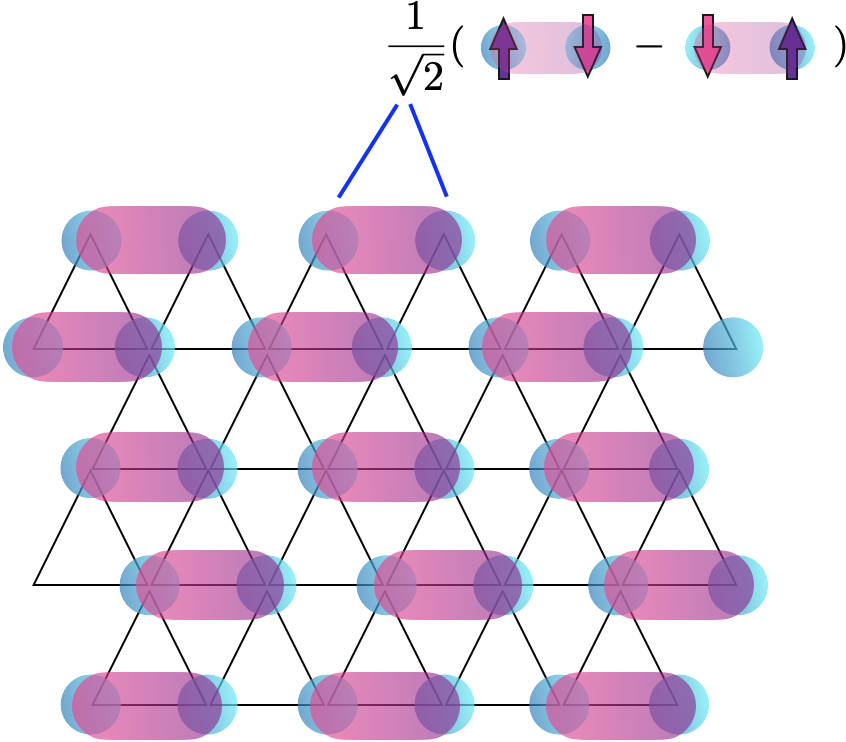
Chevauchement quantique
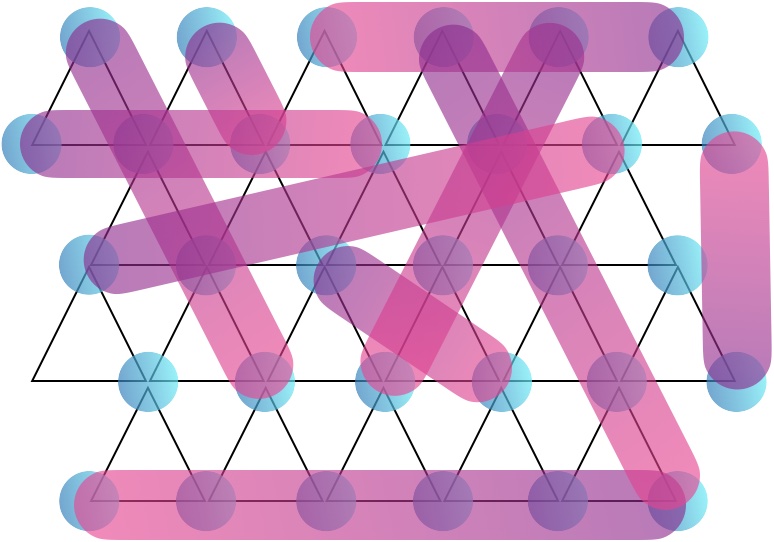
La glace de spin est un exemple d’un tel système magnétique, où les fluctuations empêchent l’ordre à longue portée avec une symétrie brisée de s’établir, même au zéro absolu. Les systèmes pour lesquels les fluctuations de la mécanique quantique empêchent l’ordre sont appelés liquides à spin quantique (QSL). La distinction caractéristique entre les QSL et les liquides ordinaires est que les fluctuations des QSL ont des dépendances de puissance à longue portée, alors que dans les liquides ordinaires, les corrélations ont une courte longueur de corrélation, qui décroît de façon exponentielle. En conséquence, les spins dans un QSL sont intriqués mécaniquement quantiquement sur de longues distances. Ce qui rend ces systèmes intéressants à étudier, c’est qu’ils nous offrent la possibilité de rechercher de nouveaux états fondamentaux de la mécanique quantique, avec de nouvelles statistiques quantiques.
 en_US
en_US